Note :: Tuning the Violin (determining the frequency) and Setting the Tuner App
- Hwang, Il-Seok

- Nov 15, 2021
- 6 min read
Updated: Nov 19, 2021
Learn how to determine the pitch (frequency) of each note and how to set up the smartphone tuner app for precise tuning.
View as PDF
Download PDF version
Accurate tuning is the most basic thing in violin performance and research. This time, think about how to determine the pitch (frequency) of other notes after tuning the four strings of the violin, and how to set up the tuner to tune exactly to the set pitch.
1. Determining the Frequency of Violin Notes
Just intonation refers to setting the scale by continuously stacking up perfect fifths or perfect fourths from the asic note. When A is the basic note, it is like A → E → B → F♯ → C♯ → G♯ → D♯ → A♯ → F → C → G → D → A. However, in this case, as everyone knows, there is a problem that when A is reached again, the A is ifferent from the A at the beginning. (To be precise, the two A do not have an exact octave relationship.) In the case of a violin, the strings E, A, D, and G should be tuned so that they are a perfect 5th to each other based on the A string. However, with the above method (tuning order), D and A strings are out of perfect fifth. Therefore, in a violin, the E, A, D, and G strings are first tuned to make a perfect fifth. If it’s tuning for a performance, this is the end. But what I want to talk about now is about other notes.
As seen above, in just intonation, the pitch changes according to the order in which the pitch is determined. For the player, if only four open strings are tuned, the other notes are played while the player adjusts them appropriately, so there is no big problem. However, it is different for researchers. This is because, of course, the height (frequency) of all notes must be clearly determined for accurate analysis and research. However, since there is no absolute correct answer for pitch, this study intends to determine the frequency for each note in the most appropriate way within the limit that does not deviate from the principle.
First, when a fundamental tone is given, the method of calculating the frequencies of notes having a relationship of a perfect fifth or a perfect fourth with the fundamental is as follows.
Two notes in a perfect fifth have a frequency ratio of 2:3. Therefore, to obtain the frequency of a sound that is a perfect 5th above the reference sound, multiply the frequency of the reference sound by 3/2. For frequencies below a perfect fifth, multiply by 2/3. Likewise, since a perfect fourth has a frequency ratio of 3: 4, the upper note is multiplied by 4/3, and the lower note is multiplied by 3/4. For example, when the frequency of A4 is 440, the frequencies of notes in the relationship between perfect fifths and perfect fourths are calculated as shown in
Figure 1.

Figure 1: Calculating the frequencies of perfect fifths and perfect fourths in A4
When calculating the frequencies of all notes using the above calculation method, proceed as follows.
1. A4 frequency determination
2. Calculate D, which is a perfect fifth, based on A4
3. Calculate G, which is a perfect fifth based on D
4. Calculate E, which is a perfect fifth, based on A4
In this way, the open strings of the 4 strings are determined (the same as the tuning order of the 4 strings), and the frequencies of the remaining whole notes are calculated based on this.
5. Calculate in order of C → F starting with G
6. Calculate B starting with E

Figure 2: Calculation of whole tones
All the whole tones were determined above. Next, a semitone must be decided, and the frequencies of the semitones are all changed depending on which tone is used as the standard. I took the method of finding F♯ → C♯ → G♯ sequentially based on B, and finding A♯ → D♯ sequentially based on F. Starting with B, if you find the perfect fifth in order, you can get both A♯ and D♯ just like F♯ → C♯ → G♯ → D♯ → A♯. However, the reason it is divided into two as above is because if you connect and stack them all at once, the error at the last note becomes too large. To summarize:
7. Calculate in order of F♯ → C♯ → G♯ starting with B
8. Calculate in order of A♯ → D♯ starting with F

Figure 3: Calculation of semitones
Figure 2 and Figure 3 are diagrams of the above sequence for better understanding. Circular numbers indicate the order of calculation.
The frequencies of the notes calculated by the above method are shown in Table 1.

Table 1: Frequency of violin notes
2. Tuner App Settings
You won’t need a tuner if you have absolute pitch, or if you’re tuning to other instruments. However, in most cases, a tuner is required, and for researchers, a tuner is a must.
Unlike in the past, there is no need to purchase a tuner these days, and you can easily tune using an app if you have a smartphone. As a result of testing many tuner apps, there were only two apps that I personally found useful (not all apps were tested), and other apps had various problems. For example, even though it is a violin tuner, it is set to equal temperament, or if it is set to just intonation but the E, A, D, and G strings are not in perfect fifth. Other than that, only 4 notes of E, A, D, and G can be identified, or the frequency is not marked.
Excluding these apps, the only surviving apps are ‘gStrings’ and ‘Cleartune’. These two apps were developed in the early days of smartphones, and they are also the oldest and have the most users. When tuning using a smartphone app, the biggest concern is the accuracy of the measurement. However, in actual testing, no problems were found in the above two apps. (more accurate than expected) Therefore, below, I would like to explain the above two tuner apps.
⃝ Cleartune
‘Cleartune’ has no regrets except that the letters indicating the frequency are displayed too small. The most important temperament setting, starting with equal temperament, has all the temperament options such as the just intonation for strings, the pythagorean just Intonation, and meantone temperament. What I need is a just intonation for strings, and when this option is selected, the frequency of each note is exactly the same as the value I calculated above.
⃝ gStrings
Unlike ’Cleartone’ above, ’gStrings’ has a large letter indicating frequency, so visibility is good. However, ‘gStrings’, like ‘Cleartune’, provides various temperament options, but just intonation for strings does not. Nevertheless, I usually use these ‘gStrings’. The reason is that I can customize the temperament myself. That is, I can modify all temperament options, and I can create my own temperament.
Therefore, below, we will learn how to create your own temperament in ‘gStrings’, the final destination of this chapter.
Click the triangle symbol at the bottom of the screen to enter the settings screen
Select Instrument > Violin, and exit to the setup screen again.
Click on Temperament
Click the ’+’ sign at the bottom right to create a new temperament
Enter the name of the temperament (My Violin, etc.)
Enter the appropriate number from A to G♯ and press the arrow at the top to exit the setting screen.
On the temperament selection screen, select the temperament you just created and press the arrow at the top again to exit from the setting screen.
The temperament you just created appears at the bottom of the screen.
‘gStrings’ is based on equal temperament, and other temperaments set how many cents to increase or how many cents to decrease based on the equal temperament. (If you enter the setting screen of equal temperament, you can see that the pitch values of the notes are all set to ’0’.)
Therefore, in the newly created temperament, an appropriate correction value should be input for each note. Table 2 below is the cent correction value to make all note frequencies the same as Table 1. Enter the values below into ‘gStrings’ and exit by clicking the arrow at the top.

Table 2: Setting ‘gString’ Option Values
The following Figures 4 and 5 are the actual gStrings setting screens, and you can set them in order by following the indications.
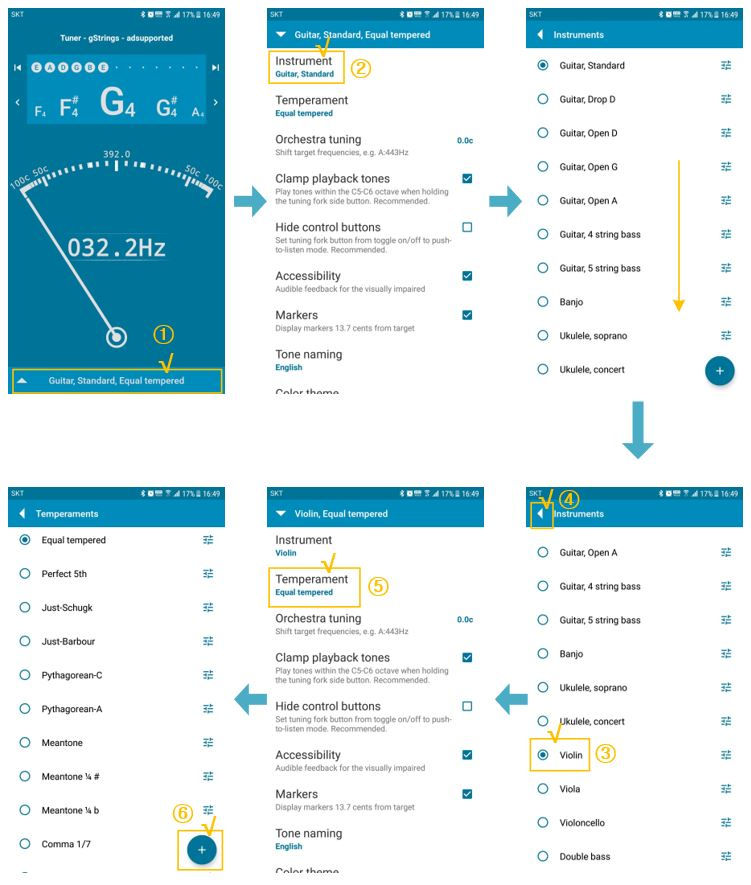
Figure 4: gStrings set - 1

Figure 5: gStrings set - 2

Comments